My daughter was counting hooks in a line, but she did something interesting. As she counted hooks, she counted the spaces between hooks, so that the next space had the same number as the previous hook. Perhaps the ordinary way to think of the space between hooks is the same—as zero—that doesn’t change the count, but she felt, quite unprompted by me, that each space was unique in its place between 1 and 2, 2 and 3, etc—That it had an identity. Normally identity in math is denoted with “=”. Expressing the identity of 1 is done by writing “1=1” or 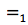. A space is the opposite of an object, but the difference between hook 1 and hook 2 could be thought to have an identity, because it can be identified with its context between hook 1 and hook 2, for example, and could be written  . It was in Plato’s The Sophist that it was offered that not-being be the spaces or differences between beings. The inequality, or difference, between 1 and 2, , or between 2 and 3 are such spaces.

I am contrasting a definition of number as a difference with a common belief that a number is a class or likeness of members. Normally the number three is essentially a set of three members, where the members of the set could be any three things we wish to collect or associate. However, we run into difficulty when five year old children count spaces instead of objects. What do the spaces have in common, how can they be identified, except as differences between objects? And in that case, how are we to deal with the idea that three “spaces” share a likeness, when all they are is purely a difference?

The point of this is to argue that different differences (or inequalities) are different from each other. Put simply

As argued in a previous post (https://questionsarepower.org/2015/01/31/degrees-of-difference/), the difference between 1 and 2 is different from the difference between 2 and 3, even though 2-1=1 and 3-2=1, we have to keep the context of the first and second subtractions with their results.

To return to that argument briefly, observe how the difference between age 1 and 6 is much greater than the difference between age 40 and 45, even though the distance between each set is 5. Further, one difference between and circle and a square is that the square can be triangulated while the circle cannot, but this difference can be turned into a similarity between a square and a strict rectangle. This would suggest that a difference “=” a likeness. Back to our inequality above, that we could denote the first difference “2-1” with ,and the second difference “3-2” with ,. If we were to lose these contexts and allow both to be reduced to the same “,” contradictions would follow. For example if we were to lose the contexts in the inequality

by writing simply

In English, the idea that something “does not equal ”, reduces to “=”, so we replace two of the “not-equals” with one “equals”:

Now, what is  equal to?

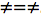Since we already know , it cannot be that . That would be a contradiction, but the alternative:

Is also a contradiction.

So we cannot lose our context for differences, and must be aware of the difference between differences. The symbols “” and “1”  are misleading because they erase their contexts including if “1” is a difference or identity. This means, apart from the current context-wanting misuse of the inequality sign, that difference, variation, diversity are not universal, they cannot be generalized. Instead difference is always special to its context. Difference is not a neutral term, because it always implies a discrimination between particular persons, places, or things.

Complementary to this vein, and in defense of its pedagogy, an aging Augustus De Morgan wrote an essay in which he tried to generalize the “=”. (Augustus De Morgan, “On Infinity and on the Sign of Equality,” Trans. Cambridge Phil. Soc. 1871, II:145-189.) The problem he faced was:

On generalizing and replacing 0 with x we run into some trouble. De Morgan’s philosophy and historicity of mathematics was such that he felt great mathematical progress was found in “mangled” (Pickering 2006) algebra. (Richards, 1987) The trouble was not that the steps were incorrect, but how to interpret the steps so that the symbols were about something. Understanding a generalized = is one thing, and it may be that the can be generalized as above and then interpreted so that it is still about something, but I’d contend that the nature of inequality is that is is the opposite of generalization. Generalization, like an umbrella or a set, asserts a higher likeness within its domain. To assert a set A, for example, in which each of its members had some difference or other with the other members, would be like the power set of everything. Finding a contradiction or two in this set (of course it would contain Russell’s Paradox) shouldn’t be too hard.

So I’ll do it here: the set A, whose members have some difference from all the other members of the set, must contain itself (A in A), since A, the set, is not like any other member of A. This means that the property that defines the set and that the members of A share, that of being different, is not shared by any member of the set. -><-

Read more here: https://questionsarepower.files.wordpress.com/2016/03/many_roads_from_the_axiom_of_completenes-2.pdf

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.